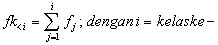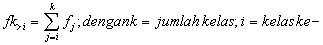Sebaran Frekuensi
Sebaran frekuensi adalah pengelompokan data ke dalam beberapa kelas. Sebaran frekuensi umumnya berbentuk sebuah tabel. Dalam suatu tabel frekuensi (atau sebaran frekuensi) dapat berisi informasi tentang jumlah atau disebut frekuensi, frekuensi relatif, frekuensi kumulatif kurang dari dan frekuensi kumulatif lebih dari.
Berikut ialah contoh suatu sebaran frekuensi :
|
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
|
Bobot (kg) |
Nilai tengah (M) |
frekuensi |
fr |
fk< |
fk> |
|
7 – 9 |
8 |
2 |
0,04 |
2 |
50 |
|
10 – 12 |
11 |
8 |
0,16 |
10 |
48 |
|
13 – 15 |
14 |
14 |
0,28 |
24 |
40 |
|
16 – 18 |
17 |
19 |
0,36 |
43 |
26 |
|
19 – 21 |
20 |
7 |
0,14 |
50 |
7 |
Keterangan :
Sebaran frekuensi di atas terdiri atas 5 kelas. Kelas I adalah data dengan bobot antara 7 kg sampai dengan 9 kg. Kelas II adalah data dengan bobot antara 10 kg sampai dengan 12 kg, dst.
Kolom (1)
Angka 7, 10, 13, 16, dan 19 disebut dengan Batas Bawah atau Lower Limit (LL)
Angka 9, 12, 15, 18, dan 21 disebut dengan Batas Atas atau Upper Limit (UL)
Kolom (2)
Nilai tengah untuk masing-masing kelas, dicari menggunakan rumus :
Mi = (LLi + ULi) / 2 ; dengan i = kelas ke-
Kolom (3)
Jumlah atau frekuensi untuk setiap kelas.
Kolom (4)
Frekuensi relatif dari masing-masing kelas, didapatkan dengan menggunakan rumus :
fri = fi / n ; dengan n = jumlah data ; i = kelas ke-
Kolom (5)
Frekuensi kumulatif kurang dari yaitu penjumlahan bertambah frekuensi dari setiap kelas, didapatkan dengan rumus :
Kolom (6)
Frekuensi kumulatif lebih dari yaitu pengurangan bertahap frekuensi dari total data untuk setiap kelas, didapatkan dengan rumus:
Dari suatu sebaran frekuensi dapat dibentuk tampilan grafik. Biasanya grafik yang dibentuk dari suatu sebaran frekuensi adalah histogram frekuensi, poligon frekuensi, dan ogive(poligon frekuensi kumulatif).
Tags: sebaran frekuensi
Bahan Kuliah | denny_dhs, November 7, 2008 10:32 pm
