Pengujian Hipotesis SPSS
Pada bagian ini akan dibahas pengujian beda dua nilai tengah. Perhatikan contoh kasus berikut :
Kasus 1 : Seorang manajer penjualan akan menilai kinerja sales coordinator daerah A dan B (ceteris paribus). Di bawah ini disajikan data penjualan masing-masing salesman/salesgirl (dalam juta rupiah):
Daerah A : 10 8 9 11 12 14 6 12 9 11
Daerah B : 8 9 8 10 12 10 8 6 8 13
Siapakah yang memiliki kinerja paling baik apakah sales coordinator daerah A atau daerah B ? Asumsikan ragam tiap daerah ialah sama (equal variance)
Untuk menjawab pertanyaan tersebut menggunakan SPSS maka lakukan langkah-langkah berikut :
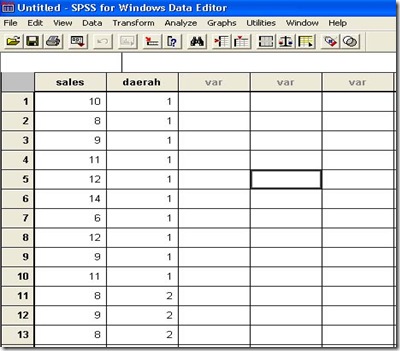
1. Input data tersebut menggunakan metode yang sudah dipelajari pada Penyiapan Data. Supaya data tersebut dapat dianalisis maka perlu sedikit dimodifikasi menjadi sebagai berikut :
Sales : 10 8 9 11 12 14 6 12 9 11 8 9 8 10 12 10 8 6 8 13
Daerah : 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2
Nilai 1 dan 2 pada daerah menunjukan kelompok data pertama dan data kedua. Nilai 1 artinya daerah A, Nilai 2 artinya daerah B. Hasil penginputan data tersebut seharusnya nampak seperti gambar di bawah ini :
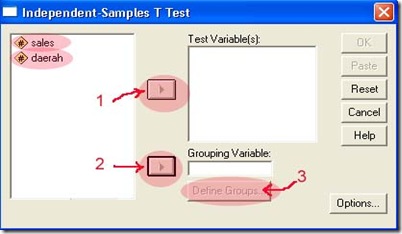
2. Berikutnya klik menu Analyze, Compare Means, Independent-Samples T Test. Pada layar akan muncul kotak dialog sebagai berikut :
3. Kemudian arahkan kursor ke sales, selanjutnya klik segitiga (angka 1) untuk memindahkan sales ke kotak Test Variable(s). Berikutnya arahkan kursor ke daerah dan klik segitiga (angka 2). Selanjutnya klik Define Groups (angka 3). Pada layar akan muncul kotak dialog sebagai berikut :
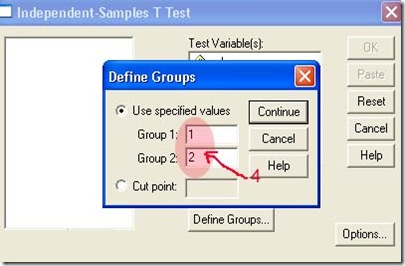
4. Pada Group 1: ketikan 1 dan pada Group 2 ketikan 2. Klik Continue. Berikutnya akan muncul kotak dialog sebelumnya, klik OK. Selanjutnya akan muncul output windows sebagai berikut :
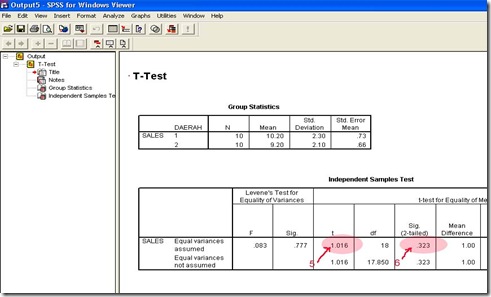
5. Angka 5 pada gambar di atas menunjukan nilai t-hitung = 1.016 dan Sig. (2-tailed) = 0.323. Artinya jika kita membuat hipotesis sebagai berikut (pada taraf nyata 5 %):
H0 : Tidak ada perbedaan nilai tengah penjualan antara daerah A dengan daerah B
H1 : Terdapat perbedaan nilai tengah penjualan antara daerah A dengan daerah B
maka dapat disimpulkan H0 diterima artinya “Tidak ada perbedaan nilai tengah penjualan antara daerah A dengan daerah B”. (Bandingkan sig. (2-tailed) dengan taraf nyata, jika sig. >= taraf nyata maka terima H0, jika sig. < taraf nyata maka terima H0)
6. Pertanyaan Kasus 1 di atas dapat dijawab bahwa kinerja antara sales coordinator daerah A dengan daerah B adalah sama.
7. Anda dapat menyimpan output di atas dengan mengklik menu File kemudian pilih save. Isikan nama yang dikehendaki. Atau anda dapat langsung menyalin output di atas ke microsoft word dengan cara klik T-Test di kotak sebelah kiri atas, kemudian pilih menu Edit dan copy object. Kemudian buka ms-word dan ketik Ctrl-V.
Tags: Tutorial SPSS
Tutorial | denny_dhs, December 20, 2008 6:29 pm
aconkcaonk — November 2, 2009 @ 10:59 pm
thanks untuk info.ny untuk spss 17 sama aj kan yh!!!
sahreeeeer — January 3, 2010 @ 10:23 am
Saya ingin nanya seandainya kalo kasusnya membandingkan makanan (4 jenis makanan) yang di suka kelompok A dan B.
Misalkan datanya: dari kelompok A (20 orang): 5 suka makan bebek, 12 suka makan ayam, 3 suka makan kambing. Kelompok B (20 orang): 7 suka makan bebek, 10 suka makan ayam, 3 makan kambing. Dua-duanya tidak ada yang suka makan sapi (0).
Pada kasus ini bagaimana uji spss-nya. Terima kasih.
admin — January 13, 2010 @ 8:50 am
@sahreeeeer : Ada banyak cara, kalo ingin dibandingkan satu-satu : misalkan dari kesukaan makan bebek; bisa dilihat apakah proporsi kel.A dan kel.B sama (gunakan uji proporsi). Atau jika ingin dilihat scr keseluruhan apakah kesukaan kel.A dan B sama atau berbeda bisa digunakan analisis ragam (anova) mgnk rancangan percobaan.
pranasta — April 11, 2010 @ 6:40 am
trus gmn dg yg 1-tailed?
apa cr ngitungnya sama ajah? atau beda dg yg 2-tailed?
misalnya:
h0= CR tdk ada pengaruh trhdp DPS
ha= CR memiliki pengaruh positif thdp DPS
tq…